728x90
이진 트리(Binary Tree)란?
- 모든 노드들이 둘 이하(0개, 1개, 2개)의 자식을 가진 트리
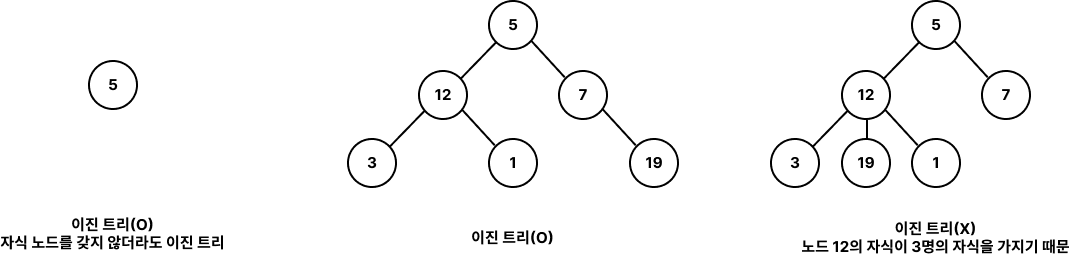
- 이진 트리의 형태에 따라 명칭이 달라짐

- 정 이진 트리(Full Binary Tree)
- 각 노드가 0개 혹은 2개의 자식 노드를 가진 트리
- 즉, 모든 노드가 자식을 완전히 가지거나 아예 가지지 않는 구조
- 완전 이진 트리(Complete Binary Tree)
- 마지막 레벨을 제외한 모든 노드가 가득 채워진 트리
- 마지막 레벨의 노드는 전부 채워져 있지 않아도 되지만 노드들이 왼쪽부터 차례대로 채워져야 함
- 이 구조는 힙(Heap) 자료구조의 조건과도 관련 있음
- 포화 이진 트리(Perfect Binary Tree)
- 모든 노드가 2개의 자식을 가지며(정 이진 트리) 모든 리프 노드가 같은 레벨에 위치하는 트리
- 모든 레벨의 노드가 채워져있기 때문에 자식 노드의 개수가 2의 제곱수만큼 증가(2^k+1 - 1)
- 예를 들어, 높이가 2인 포화이진 트리일 경우 2^3 - 1로 총 7개의 노드를 가짐
(루트 노드의 높이는 0)
이진 트리의 장단점
이진 탐색 트리(Binary Search Tree, BST)란?
- 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리
- 왼쪽 자식 노드의 값 < 부모 노드의 값 < 오른쪽 자식 노드의 값이라는 규칙이 성립되며, 중복되는 값을 허용하지 않음
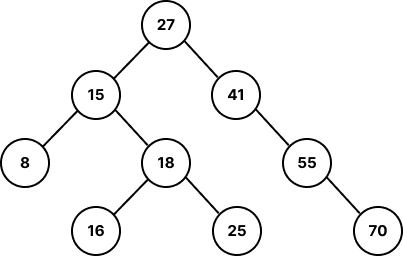
이진 트리와 이진 탐색 트리에 대한 설명을 해야하는 면접 질문
- 이진 트리(Binary Tree)
- 모든 노드가 최대 두 개의 자식 노드를 가진 트리 구조이며, 노드의 크기나 정렬 규칙이 없는 일반적인 트리 형태로 주로 데이터의 계층적 구조를 표현할 때 사용
- 특별한 조건 없이 모든 노드가 0개, 1개, 2개의 자식을 가질 수 있는 트리 구조
- 이진 탐색 트리(Binary Search Tree)
- 이진 탐색 트리는 이진 트리의 일종으로 '왼쪽 자식 노드는 부모보다 작고, 오른쪽 자식 노드는 부모 보다 큰 값을 가진다'는 규칙을 가짐
- 이러한 구조 덕분에 특정 값을 빠르게 찾을 수 있어 탐색과 정렬에 유리하며 평균적으로 O(log n)의 시간 복잡도로 데이터 검색에 효과적
728x90
'Computer Science' 카테고리의 다른 글
| [알고리즘] 자주 사용하는 정렬 (0) | 2024.11.05 |
|---|---|
| [자료구조] 해시맵 개념과 해시 충돌 (0) | 2024.11.04 |
| [자료구조] Queue 개념 (0) | 2024.11.02 |
| [자료구조] Stack 개념 (0) | 2024.11.01 |
| [자료구조] 배열(Array) (0) | 2024.10.28 |



